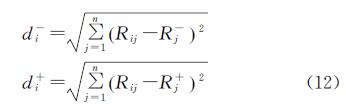2.2 高标准基本农田建设时序安排
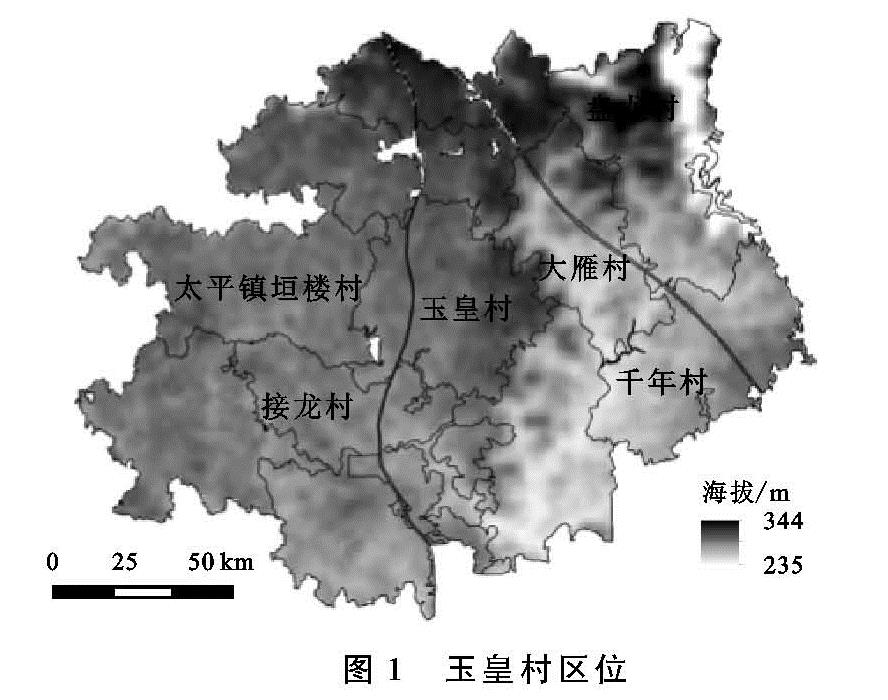
通过对玉皇村耕地自然禀赋、空间区位、社会经济以及景观形态等条件综合评价,利用理想点逼近法对该村高标准基本农田进行建设的时序安排。
2.2.1 评价指标体系构建
依据《高标准基本农田建设标准》这一纲领性文件提出的六点质量要求,以科学性、可行性、层次性、系统性和可比性为原则,从自然禀赋、空间区位、基础设施和景观形态条件4个维度构建高标准基本农田建设条件评价指标体系。
(1)自然禀赋是耕地综合质量的基础,自然禀赋的优劣决定耕地生产能力高低,对提高农业产出效益有重要作用。最终选取坡度、地下水位、土壤剖面构型、有效土层厚度、pH值、有机质含量和距坑塘水面距离等8个指标反映耕地的自然禀赋。
(2)基础设施条件可反映高标准基本农田建设设施配套能力和抗灾能力特性。本文选取灌溉保证率和排水体系健全程度两个指标反映该区域耕地基础设施条件和社会经济层面属性。
(3)地理位置和道路通达度等耕作环境因素都将对村民土地利用行为产生一定影响[25]。因此,本文选入城镇中心影响度(距城镇中心的距离),耕作距离(距居民点距离)以及道路通达度(距农村道路距离)3项因子进行量化分析,反映耕地在空间区位的适宜度。区位条件越优,农户耕作就越便利,可减少较多人力和运输成本,也可提高商品化率,提高农民社会经济效益产出。这3项因子数据可通过ArcGIS的近邻分析工具获取,由于均属于扩散型指标,因此采用衰减法赋值[26]。城镇中心影响度与耕作距离均计算点之间距离,采用指数衰减法赋值见式(1); 耕作便利程度是计算距线状要素距离,利用直线衰减法赋值见式(2)。线状指标影响半径可通过算数平均分割法得到,见式(4):
Fi=M(1-r)i(1)
Fi=Mi(1-r)(2)
r=di/d(3)
d=S/2L(4)
式中:Fi是第i个评价单元作用分值; Mi是规模指数; r为相对距离; di为图斑至道路实际距离(m); d为线状指标影响半径(m); S为研究区域面积(m2); L为路长(m)。
(4)为提升耕地社会、经济和生态综合效益,需考虑更多景观形态因素,使得高标准基本农田建设更好地服务于构建山水林田湖生命共同体。因此本文选取集中连片程度、田块分维度和斑块面积形状指数作为反映耕地景观形态的指标。
集中连片度:耕地连片度反映图斑在空间邻近集中程度,集中连片程度越高,越有利于农业规模化、机械化经营,反映高标准基本农田“集中连片”质量要求。因田间道路和沟渠等现状地物阻碍耕地集中连片,本文采用GIS分析中的空间连片性计算法,对图斑10 m以内进行缓冲分析形成缓冲区,图斑面积阈值利用ArcGIS的自然分级功能确定,集中连片程度由缓冲区面积标准化处理后结果反映,标准化计算方法如下:
q={20 s<14 hm2
20+80(s-14)/(26)14 hm2≤s≤40 hm2
100 s>40 hm2(5)
式中:q为连片度; s为耕地图斑缓冲区面积(hm2)。
田块分维度:田块分维度是不规则几何形状的非整数维度,是对耕地图斑形状复杂程度进行度量及反映的结果,为逆向指标。其反映田块形状规整程度,田块规整有利于农业机械耕作,且有助于强化乡村景观质量提升,满足乡村振兴战略要求。公式如下:
Fd=2ln(P/k)/ln(A)(6)
式中:P为图斑的周长(m); A为图斑的面积(m2); Fd为分维数; k为常数。
面积形状指数:图斑面积形状指数通过计算某一图斑形状与同样大小的圆或正方形之间的偏离程度来测算其形状复杂程度,在一定程度上反映了耕地景观质量高低。耕地图斑形状整齐有利于生产管理、田间排灌及机械化作业。结合玉皇村实际情况,本文选择以正方形为参照几何形状,进行图斑面积形状指数计算。图斑形状面积指数越大,越扁长、越复杂,景观质量越低。计算公式如下:

式中:S为斑块形状指数; P为图斑周长(m); A为图斑面积(m2)。
2.2.2 指标无量纲处理
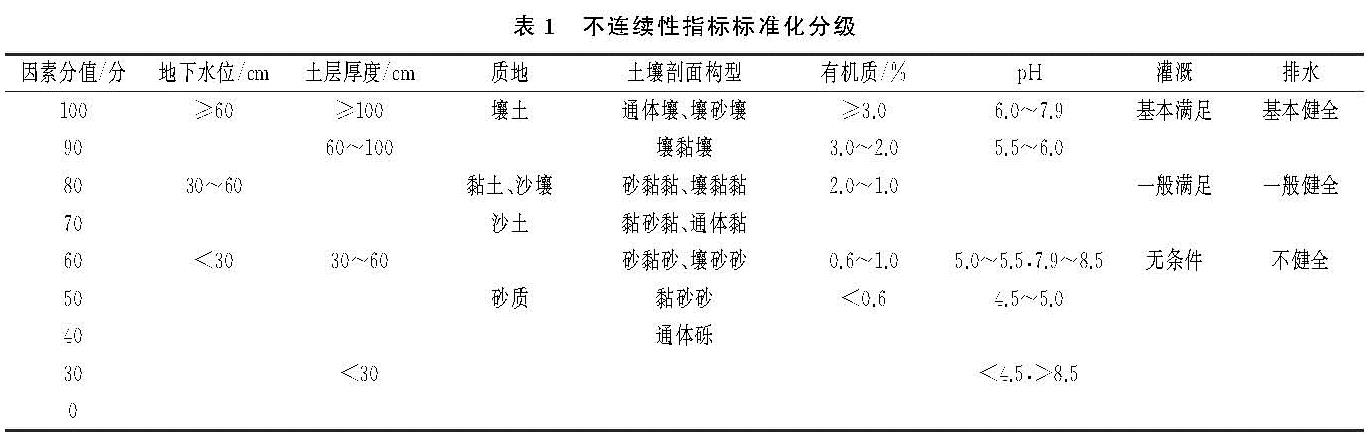
玉皇村耕地共有267个评价单元参与评价,连续性指标采用极值法进行无量纲化处理,不连续指标采用[0,100]赋值法处理,见表1。
2.2.3 建设时序区域划分
(1)构建标准化决策矩阵x:玉皇村耕地共有267个评价单元xi{i=1,2…,m},16个指标xj{j=1,2…,n}参与评价,对数据进行标准化处理,组成规范化决策矩阵Xij:
x=(xij)m×n[x11 x12 … x1n
x21 x22 … x2n
x11
xm1 xm2 … xmn](8)
(2)综合确定指标权重。首先基于AHP模型计算获取各指标权重,其次采用熵权法对权重进行修正,最后结合主客观综合赋权方法,提高耕地质量评价合理性,实现数据科学客观化。综合赋权方法计算公式如下:
Wi=W1iW2i/∑ni=1W1iW2i(9)
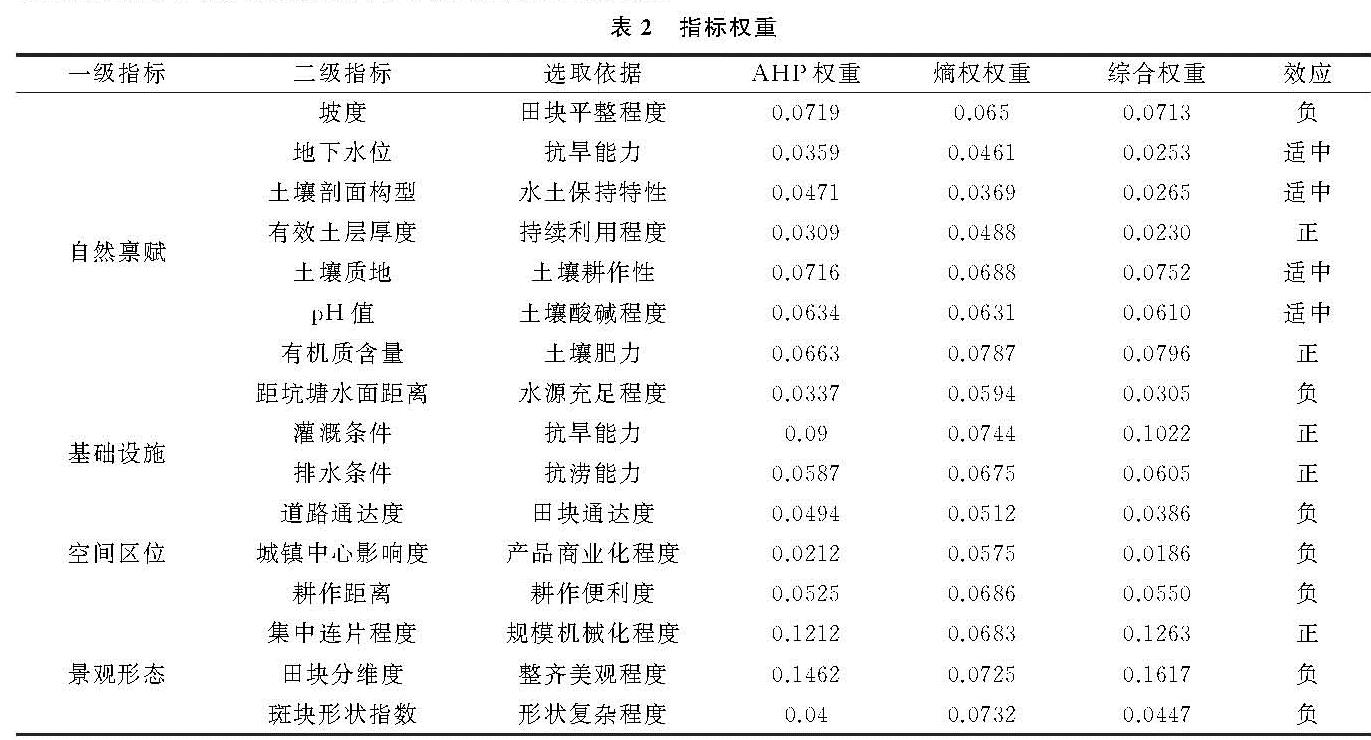
式中:Wi为指标综合权重; W1i为AHP权重; W2i为熵权[27],指标权重见表2。
(3)构造加权矩阵。由熵权法和层次分析法综合得出的指标权重gj=[g1,g2,g3,…,gn]与标准化矩阵相乘,从而构建加权矩阵R:
R=(rij)m×n=[r11 r12 … r1n
r21 r22 … r2n
r11
rm1 rm2 … rmn](10)
(4)确立正、负理想解。各项量化指标达到最大值为正理想解(R+j),反之就是负理想解(R-j)。
R-j=min(rij) R+j=max(rij)(i=1,2,…,m)(11)
(5)计算距离。在确定理想解的基础上,计算各评价单元与理想解之间的距离,计算见式12:
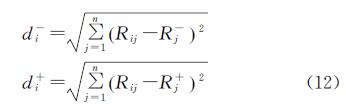
式中:d+i,d-i分别为评价对象与正理想解和负理想解的距离。d+i值越大,结果表明评价对象距正理想解的距离越远; d-i值越大,表明评价单元距负理想解越远。
(6)计算相对接近度(Cj)。衡量每一个评价单元与理想点相对接近程度,即根据现代农业发展需要,每一个耕地图斑被选为高标准基本农田建设对象的可行程度。
Cj=(d-i)/(d+i+d-i)(13)
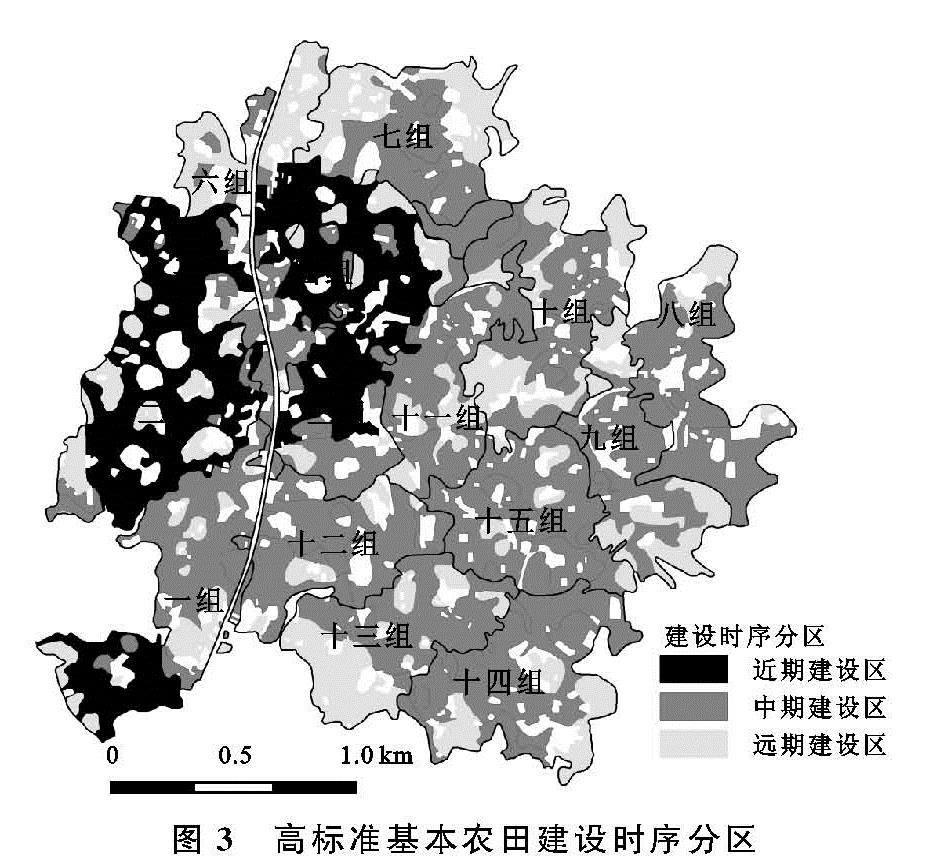
(7)高标准基本农田建设时序分区。基于Cj大小对高标准基本农田建设进行排序,Cj越大,表明该耕地越满足高标准基本农田建设要求[28]。基于GIS标准分类法自然断点功能,将玉皇村耕地划分为3个建设时序区域,分别为近期、中期和远期建设区域。
2.3 高标准基本农田整治模式分类
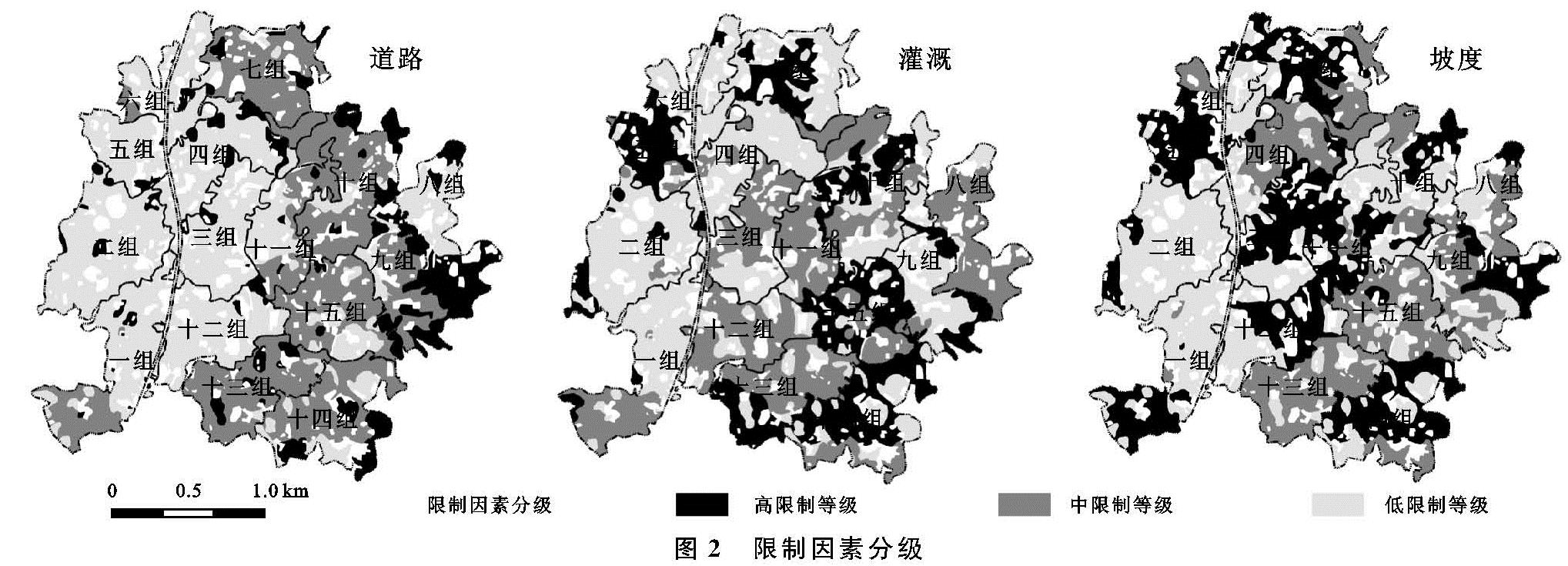
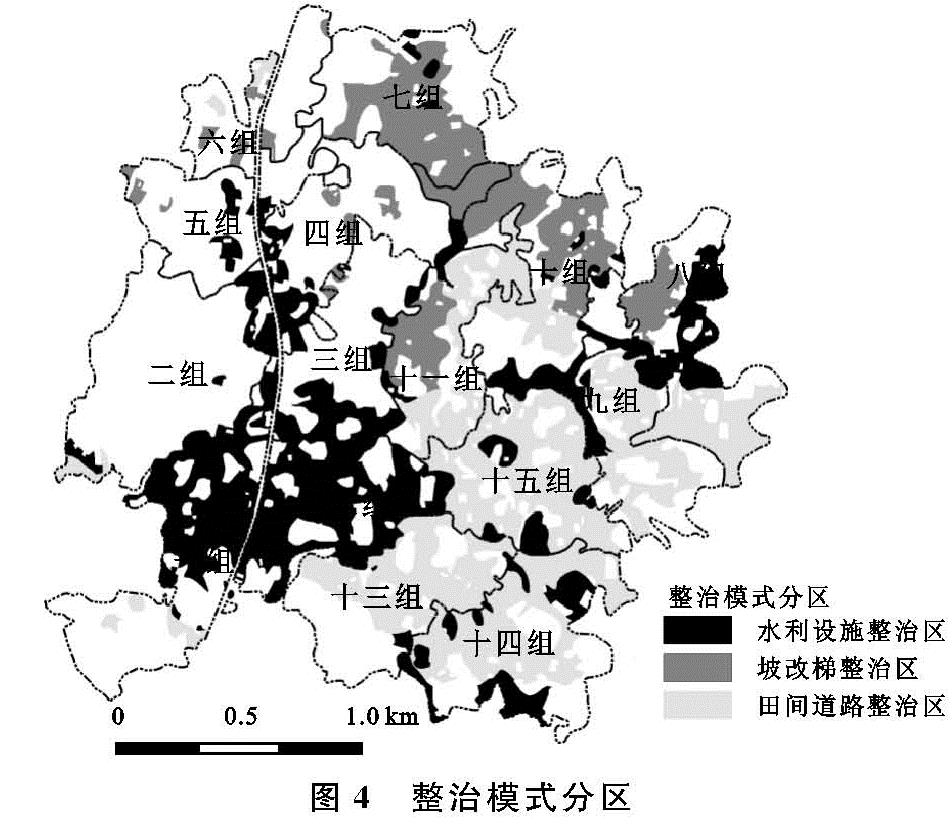
补短板并制定差异化土地整治措施可补充高标准基本农田的后备资源,推动土地利用可持续发展[29]。划分土地整治模式取决于可改造或消除的限制因子,在土地整治工程中,坡改梯、田间道路建设、农田水利设施建设是较为普遍的3种整治模式。因此本研究从田水路林村角度出发,选取坡度、灌溉保证率、耕作距离作为核心的限制因子。基于自然分等功能,将各限制因子限制程度分别划为高中低3个等级,最后利用互斥矩阵形成如“高中低”的组合,见图2,经汇总分析实际上只有21种。土地整治难度主要取决于限制因子数量和限制程度。当耕地的限制因子数量相同时,因子种类和属性决定了耕地整治改造方向,从而决定了耕地整治模式。组合的划分结果如表3所示。