1.1 研究区概况
齐齐哈尔市是东北地区工业发展的重要枢纽,也是黑龙江省西部经济、政治及文化中心。地处黑龙江省西南部松嫩平原,东经123°—126°,北纬45°—48°,总体地势平坦,北部地势较高,东部及南部地势较低; 市域内包含嫩江等主要河流廊道,本土植被主要为草甸草原。齐齐哈尔市具有典型东北地区的温带大陆性季风气候,四季分明,春季气候干旱多风,夏秋两季短暂而多雨,冬季漫长而寒冷。近年来,哈大齐工业走廊相关建设和产业发展对城市群起到了极大的经济带动作用,齐齐哈尔市以非金属矿为工业发展特色,快速工业发展使得主城区建设用地急剧扩张[20],侵占城乡生态空间,湿地、林地、草地斑块布局零散,主城区东南部与大庆市接壤的大面积湿地斑块逐渐呈现破碎化,水土流失较为严重,亟待修补与资源整合。
1.2 研究方法
1.2.1 数据来源及预处理
本研究采用的数据主要包括《齐齐哈尔市统计年鉴》、齐齐哈尔市矢量路网(源自Open Street Map)、齐齐哈尔市Landsat遥感影像与DEM高程数据(源自地理空间数据云,30 m)、高清Google影像等。下载Landsat5/Landsat8卫星在相等间隔(2003年、2010年、2017年)的三期影像以及DEM,2003年、2010年、2017年三期精度为30 m的Landsat影像均选自6—9月的无云影像,土地利用类型清晰,植被覆盖良好。通过ENVI与ArcGIS分别对三期影像进行几何校正、辐射校正、大气校正、波段融合,根据本研究需要,将土地利用类型分为湿地、林地、草地、耕地、建设用地和未利用地6类。以目视解译法根据Google Earth高清历史影像对数据进行纠错,每期随机生成200个样点,通过ENVI混淆矩阵和精度评价进行验证,得出分类精度分别为84.5%,88.0%,87.5%,平均精度为86.67%,满足后续研究需要。
1.2.2 基于MSPA方法的景观识别
形态学空间格局分析法(morphological spatial pattern analysis,MSPA)在生态源地识别方面应用较多,从生态结构连通性入手,基于数学原理对图像栅格进行空间格局的识别分析[21]。本研究基于解译出的2017年土地利用类型栅格图(像元大小为30 m),提取湿地、林地、草地作为MSPA的前景要素,因考虑耕地的人为干扰程度较强,将耕地、建设用地、未利用地设为背景,转换成tiff格式的二值图,在Guidostoolbox中识别出7种景观类型,分别为核心区、桥接区、岛状斑块、环道区、边缘区、支线、孔隙。
1.2.3 生态源地景观连通性评价
应用Conefor 2.6软件,根据斑块连通距离阈值和连通概率可计算出斑块的景观连通性相关指数。景观连通性是衡量区域生态斑块相联系程度的重要指标之一,可能连通性指数(the probability index of connectivity,PC)在现有研究中应用较多,其分析优势在于综合考虑了物种迁移能力和扩散概率,是现阶段较为成熟的评价指标; 可能连通性指数变化量(the delta values for probability index of connectivity,dPC)常用来反映斑块重要性[22],公式如下:
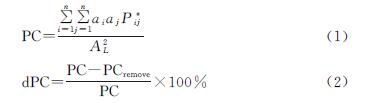
式中: n为研究区域内斑块的总数; ai与aj分别为斑块i与斑块j的面积; A2L为研究区斑块的总体面积; P*ij为斑块i与斑块j之间物种迁徙扩散的最大可能性; PCremove为将随机斑块i剔除后的景观连接度。结合前人研究[9,11,13,16],将斑块连通距离阈值设为500 m,连通概率为0.5,应用Conefor 2.6进行分析计算,根据结果筛选生态源地。
1.2.4 阻力面的构建
斑块阻力值表示物种扩散的困难程度,对生态网络构建具有重要意义。根据研究区人为干扰与实地调研情况,结合文献[23-24]对各土地利用类型进行阻力赋值,赋值范围1~100。基于MSPA方法对生境斑块的识别,生态源地是物种生存的最佳场所,面积较大,具有保护生物多样性的作用,对物种扩散几乎不产生阻力,此类土地的阻力值最小,赋值为1。其他核心区阻力值相对生态源地稍有增大,但因核心区具有较高的生态价值[23],在整体阻力中仍属于低阻力区。桥接区是核心区之间的衔接斑块,起到廊道连通的作用,促进区域信息流动,阻力较小,赋值为10~20。岛状斑块为区域生态系统中的潜力节点,但与其他斑块连通程度一般,赋值为30。除dPC值较高的核心区、桥接区外,其他草地、林地、湿地斑块面积较小、连通性差,此类土地的阻力值相对较大,赋值在30~50。耕地受到较强的人为干扰,赋值为80。建设用地为硬质表面,是人为干扰最强的区域,阻力值最大,赋值为100。
坡度与海拔对物种扩散具一定程度影响[13],阻力赋值范围为1~100。根据寒地物种栖息地的特征[25],坡度小于5°时,几乎不影响物种扩散,赋值为1。迁徙难度随坡度增加而增加,当坡度大于20°,物种迁徙较困难,此类地形阻力较大,赋值为80。海拔上,物种扩散难度随高程增加而增大。研究区域景观要素较复杂,土地利用类型在阻力面的构建中占有较大权重,坡度因子次之,因研究区处于东北平原,地形海拔较低,对物种影响较小,其权重也相对较小。综上,基于熵值法[26]计算各类指标的离散程度,分析得出土地利用类型、坡度、高程的权重分别为0.58,0.25,0.17(表1)。
1.2.5 基于MCR的生态廊道构建与优化
最小累积阻力模型(minimum cumulative resistance model,MCR)是现有生态廊道识别的有力途径[27],该模型计算源点到目标点所需克服的最小累积阻力,获得两斑块之间的最小成本路径,即物种扩散最优通道,公式如下:
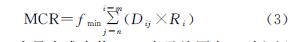
式中: MCR为最小成本值; Dij表示从原点j到空间单元i的空间距离; Ri表示空间单元i的阻力系数。
重力模型[28]能够科学评价生态源点与目标点之间的相互作用程度,相互作用力值越大,两者间的廊道在区域生态系统中具有越重要的地位。经过重力模型计算可得出区域廊道重要性分级,并对廊道稀疏地区进行补充,科学优化生态网络结构。重力模型公式如下:
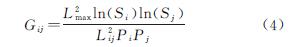
式中:Gij代表研究区域内斑块i与j之间的相互作用力强度; Si为斑块i的面积; Sj为斑块j的面积; Pi为斑块i的阻力值; Pj为斑块j的阻力值; Lij为斑块i与斑块j之间廊道的累积阻力值; Lmax为研究区域所有廊道的最大累积阻力值。
网络闭合指数(α指数)、网络连接度指数(β指数)、网络连通率指数(γ指数)反映出区域生态系统中源地与廊道的连通关系以及生态网络结构的复杂程度,指数数值与生态廊道连通性呈正相关[29-30],计算公式如下:
α=(L-V+1)/(2V-5) (5)
β=L/V (6)
γ=L/(3(V-2)) (7)
式中: L为生态廊道数; V为生态节点数。通过计算对比生态网络优化前与优化后的网络结构指数来量化网络优化结果。
1.
生态敏感性是指某区域生态系统受人类活动干扰后的环境变化程度,表示该区生态环境被破坏的可能性,高敏感区的生态效益更易因人为干扰而下降[31-32]。对优化后的“源地—廊道”生态网络体系构建多级缓冲区,结合文献[33-34]将生态网络“源地—廊道”体系50 m缓冲区内作为极敏感区,50~200 m为高敏感区,200~500 m为中敏感区,500~1 000 m为低敏感区,其余地区为不敏感区。根据结果提出相应的保护措施,为城市生态规划相关工作提供参考[35]。在生态网络建设过程中,生态断裂点的存在不容忽视[11,36]。生态网络体系与研究区域内穿行的铁路、高速路、国道相交处为生态断裂点,通过Open Street Map网站和QGIS软件获取研究区域矢量路网,在ArcGIS中与廊道叠加取交点并进行分级评价,根据结果提出相关修复建议。