2.1 降雨型滑坡稳定性系数计算模型
对于降雨型滑坡,首先要建立合适的降雨型滑坡稳定性系数计算模型,以便更精准的分析与评价降雨型滑坡稳定性。
本文没有选取边坡工程常用的简化Bishop法及瑞典条分法,而采用剩余推力法进行稳定性计算。对于滑面为任意形状的滑坡稳定性计算,采用剩余推力传递法较为合适。其考虑了滑体自重、坡面荷载、动水压力、静水压力、滑动面处的浮托力、暴雨、地震和不同条块滑面段抗剪强度参数差异对滑坡稳定性的作用和影响,见图2。
剩余推力法计算稳定性系数完整的计算公式如下:
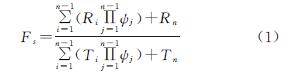
式中:Ri为第i块条块的抗滑力; Ti为第i块条块的下滑力; ψj为第i块的传递系数; Rn为最后一个计算条块的抗滑力; Tn为最后一个计算条块的下滑力。
由于降雨型滑坡需要着重考虑暴雨工况下坡体受力情况,而在降雨过程中地表水及地下水的活动使得坡体内部的水压力难以精准确定。由此构建降雨型滑坡分析模型,由图3所示。
从图3可以看出,当对暴雨条件下的滑梯前缘条块进行受力计算时,可将ABCDEFGHIA视为一个前缘受静水压力阻力作用的整体滑坡,该条块所受重力应为DEFG内所有水、岩重量总和,仿此考虑滑坡堑中受水作用的条块受力; 当水位下降时,孔隙水压力变为KIHGJ,按此水压线计算滑坡稳定性。即无论何种地表水、地下水活动情况,坡体内部地下水渗流的作用均可视为作用于各个条块边界上的静水压力。这种分析模型就可以获得任意形状滑动面在复杂荷载作用下的滑坡推力[8],并且滑动面条分后各条块的受力均可快速确定,使得降雨型滑坡在暴雨工况下的稳定性计算分析变得更为简洁合理。
2.2 滑坡破坏概率计算方法
在对滑坡Fs稳定性系数进行计算时,往往采用的是传统计算方法,计算滑坡稳定性系数的公式中需要考虑各类因素的具体确定数值,比如研究区岩土体力学性质参数C,φ值、各层岩土体的标准重度、条块划分的尺寸大小、倾斜角度以及所受各种力的确定值,由此方法计算得出的稳定性系数Fs也为一个具体确定数值。但在实际工程条件下,虽然条块划分尺寸及倾斜角度实为可测定值,但各层岩土体物理力学参数分布较为离散,并且测试过程中存在误差,各种受力的大小也会随着外界条件的改变而改变,导致无法取得其准确数值并导致计算产生极大的误差。现将滑坡稳定性系数带入概率框架进行分析,稳定性系数计算参数不为一个定值,而应视为符合某种规律分布的数值集合。当确定滑坡稳定性系数的主要影响计算参数的概率分布,利用Monte-Carlo法,通过产生随机数值带入计算参数中,使其符合概率分布,将符合概率分布的计算参数带入稳定性系数公式计算得出符合概率分布的滑坡稳定性系数[9]。对于此流程不断重复若干次,计算得出符合概率分布的稳定性系数足够多时,通过大数定律可以将此时滑坡稳定性系数属于破坏的频率视为破坏概率:
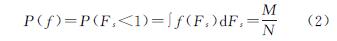
式中:N为滑坡稳定性系数总体数量; M为滑坡稳定性系数小于1的数量。
通过公式(2),对计算得出的滑坡稳定性系数总体数量N进行统计分析,便可以验证滑坡稳定性系数分布规律是否与主要计算参数分布规律一致。由于各个随机变量对滑坡稳定的影响均不相同,因此可以把影响程度较小的量作为定值以简化计算。在不确定因素中以岩土体黏聚力C和岩土体内摩擦角φ对滑坡稳定性影响最大[10],故选取这两个参数为随机变量,其他参数则作为定值来处理。由此可以建立状态方程FS=f(C,φ)。
当确定状态方程FS=f(C,φ)之后,下一步需要对岩土体黏聚力C和岩土体内摩擦角φ的概率分布进行分析。首先根据各类工程经验及研究总结广泛应用的绝大多数概率分布类型,主要有Bernoulli分布、Poisson分布、极值分布、中心极限分布及其他分布。结合各概率分布类型的特点、物理意义以及主要工程应用,发现中心极限分布与滑坡稳定性主要影响因子分布是较为契合的,并且通过许多学者的研究也表明是合理可行的。对于中心极限分布,首先需要了解中心极限定理,其描述为:如果一个随机变量由多种(数量较大)的,并且相互独立的随机因素综合影响所构成,且其中每个随机因素在总体影响中所起到的作用均十分微小,则此随机变量往往近似服从正态分布[11]。其原理如公式(3)所示:
Y=X1+X2+…+Xn (3)
式中:Y为随机变量; X1,X2,Xn为随机变量Y的相互独立影响因素。由此可以看出,当n→�SymboleB@�时,随机变量Y服从正态分布,由此可以看出,若随机变量的影响因素互相独立的影响随机变量的分布,并为相互简单叠加,即可以视为正态分布。
若各影响因素之间存在相互影响,不为简单相加方式,可以将其认为共同联合影响,类似于相乘关系,原理公式如式(4)所示:
Y=X1X2…Xn (4)
对于公式(4),两边同时取自然对数,可得:
lnY=lnX1+lnX2+…+lnXn (5)
可以看出当n→�SymboleB@�时,lnY服从正态分布,故随机变量Y符合对数正态分布。当随机变量影响因素不仅仅互相独立,而是共同作用来规范随机变量的分布可以将其认为规律分布符合对数正态分布。
在确定好概率分布模型之后,需要确定岩土体黏聚力C和岩土体内摩擦角φ的分布是否为服从正态分布。当确定滑坡岩土体参数黏聚力C和岩土体内摩擦角φ的分布符合正态分布或对数正态分布后,随机数值的抽样可以通过以下公式进行,来保证数值的范围准确及离散随机[12]:
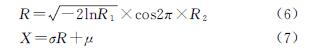
式中:R1,R2为[0,1]区间的均匀分布随机数; R为服从标准正态分布N(0,1)的随机变量; X为服从均值为μ、方差为σ的正态分布随机变量。
综上所述,破坏概率分析法的基本计算步骤如下:首先根据现场勘察和岩土体试验得出多组岩土体黏聚力C和岩土体内摩擦角φ数值,并对其分布进行判别。当确定了C和φ的分布函数基本满足正态分布之后,可利用Monte-Carlo法,采用公式(6),(7)进行抽样与变换,产生一系列满足正态分布的C,φ随机变量数值。随后将产生的一系列C,φ随机变量数值代入公式(1)中,根据具体工况对滑坡进行条块划分。确定其他基础数据后,结合剩余推力法进行计算可得出一系列相应的稳定性系数Fs的分布函数,将得到的稳定性系数分布函数带入到公式(2)中进行计算,得出滑坡破坏概率曲线,统计滑坡稳定性系数小于1时的分布密度,求出其在所计算滑坡稳定性系数中的占比,便可以求出滑坡破坏概率。计算方法流程见图4。
采用破坏分析概率模型求出滑坡稳定系数和破坏概率的数值后,可以参考按破坏概率大小滑坡稳定性等级划分表[13](表1)对滑坡稳定性进行评判。