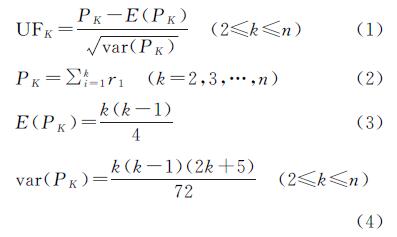2.2 研究方法
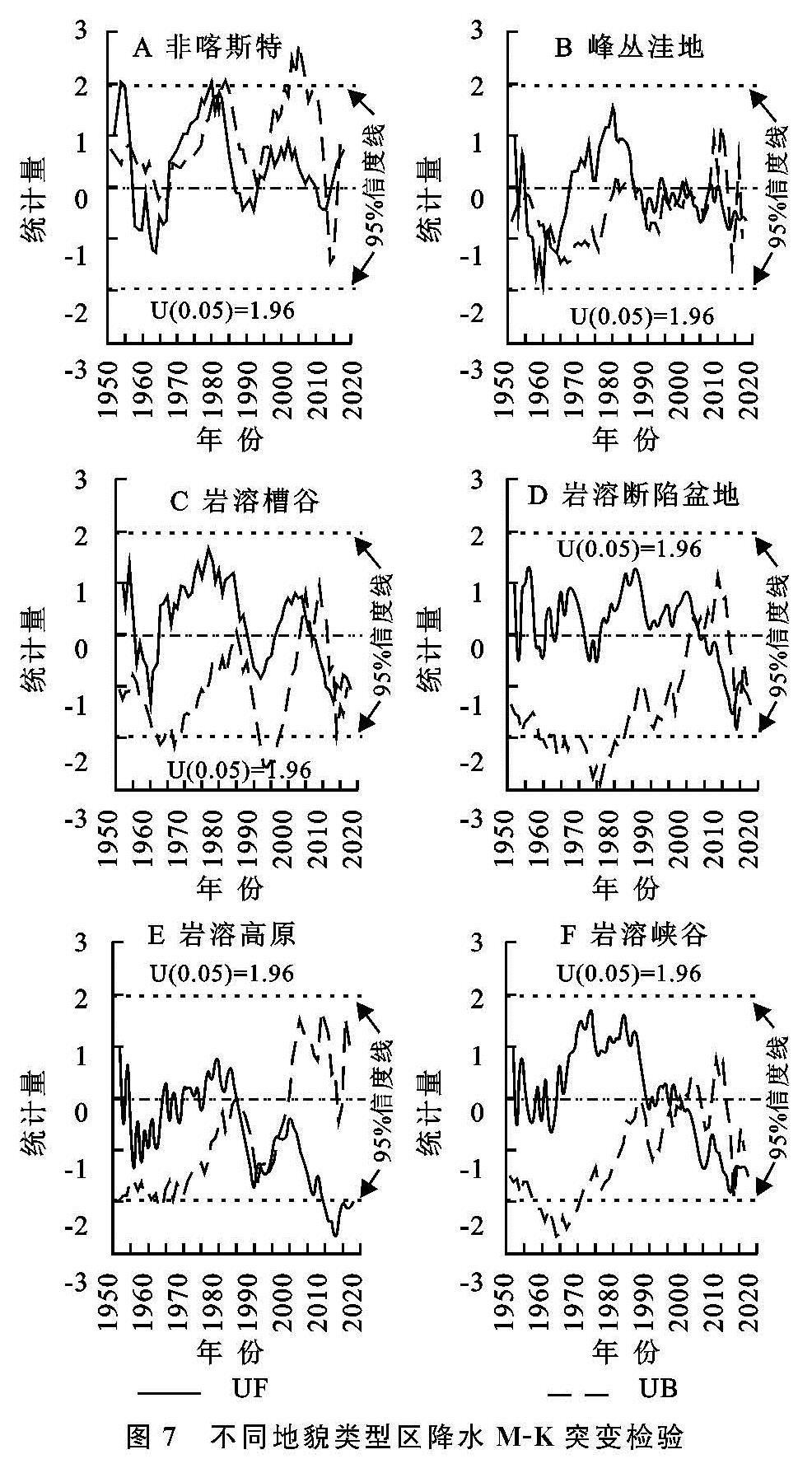
(1)Mann-Kendall检验。Mann-Kendall(M-K)[26-27]突变检验法是一种非参数统计检验方法,常用来分析降水时间序列的突变检验,假设数据序列x1,x2,x3,…,xn为平稳的时间序列,样本相对独立,其中当xi>xj时,ri=1,总累计数为FK,并定义统计量UFK,否则ri=0(j=1,2,…,i)。
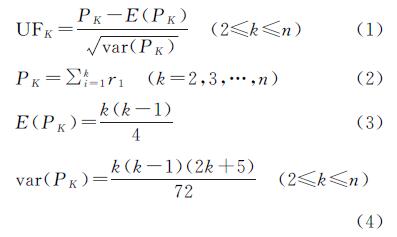
式中:PK表示第i个时刻的数值大于j时刻数值的个数的累计值; E(PK)和var(PK)分别表示累计数PK的均值和方差; 原假设为序列无趋势变化,采用双向趋势检UBK=-UFK,给定显著水平α,若|UFK|<Uα/2,接受原假设,序列存在变化趋势; 若|UFK|Uα/2,拒绝原假设,序列无变化趋势。
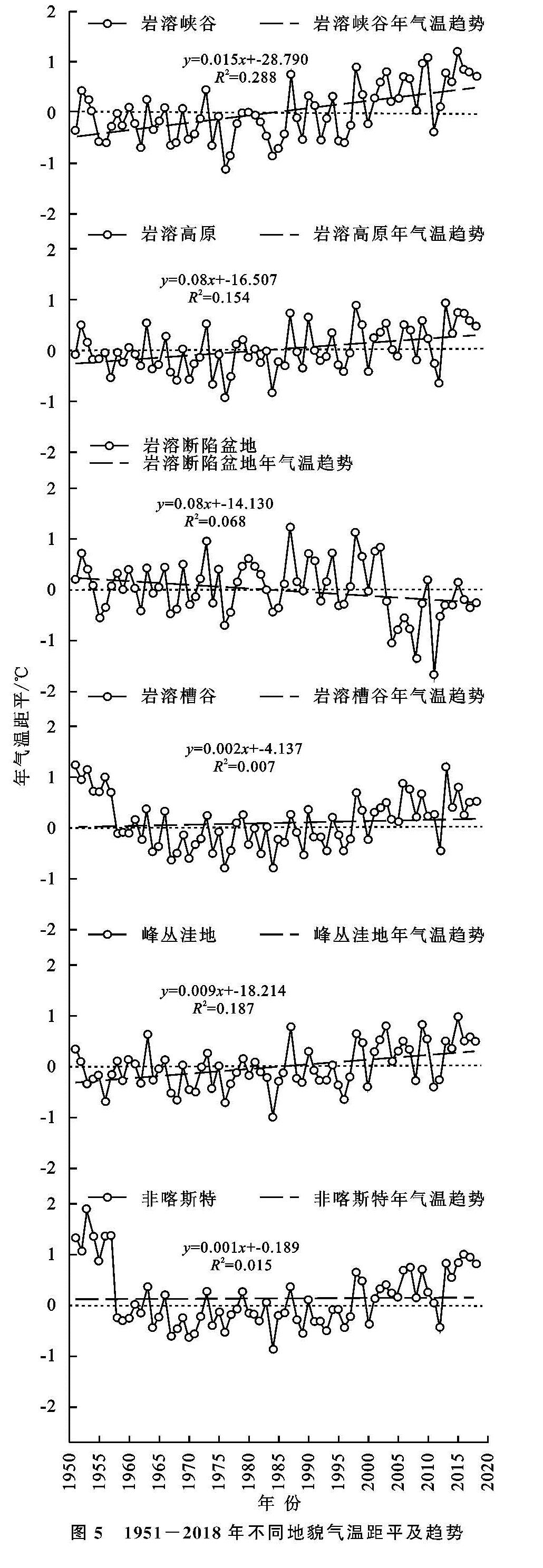
(2)滑动平均与距平累积。①滑动平均法也称为移动平均法,它的基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。因此,当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。计算公式[28]如下:
Ft=((At-1+At-2+At-3+…+At-n))/n(6)
式中:Ft表示下一期的预测值; n表示移动平均的时期个数; At-1表示前期实际值; At-2,At-3和At-n分别表示前两期、前三期直至前n期的实际值。
② 距平累积指先计算每年的降水量、气温和相对湿度距平,然后按年序累加,得到距平累积序列,计算公式[29]如下:
LPi=∑ni(Ri-R-)(7)
式中:LPi为第i年的距平累积值; Ri为第i年的降水量、气温值、相对湿度值; R-为降水量、气温、相对湿度的多年平均值。
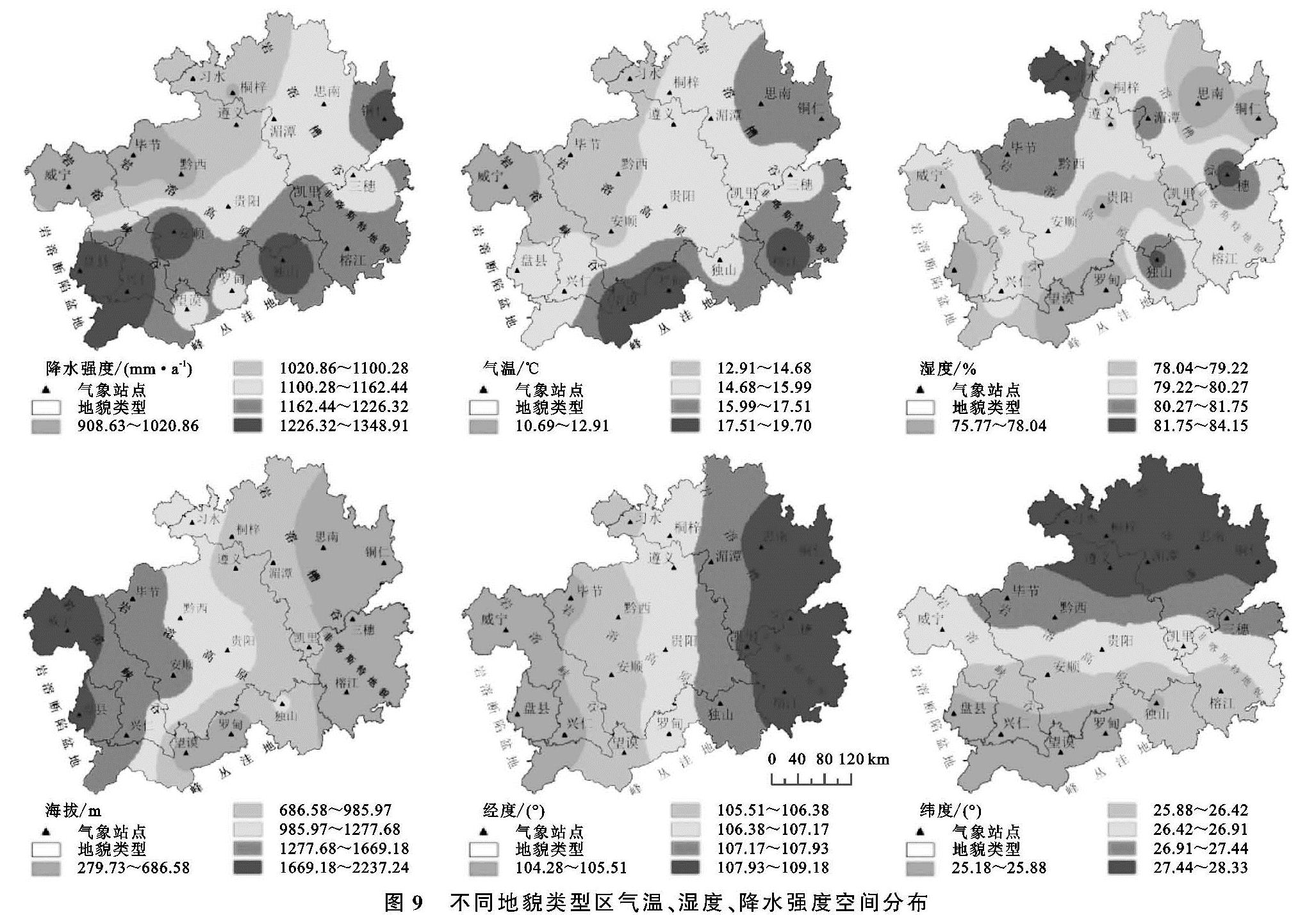
(3)反距离权重插值。反距离权重插值(Inverse Distance Weighted,IDW)[30]以插值点与样本点间的距离为权重进行加权平均,离插值点越近的样本点赋予的权重越大。设平面上分布一系列离散点,已知其坐标和值为Xi,Yi,Zi,(i =1,2,…,n),根据周围离散点的值,通过距离加权值求Z点值。
Z=[∑ni=1(zi)/(d2i)]/[∑ni=11/(d2i)](8)
式中:d2i=(X-Xi)2+(Y-Yi)2; IDW通过对邻近区域的每个采样点值平均运算获得内插单元值,它是一个均分过程,这一方法要求离散点均匀分布,并且密集程度足以满足在分析中反映局部表面变化。