1.2.1 土壤粒度测定
室内试验在兰州大学西部环境教育部重点实验室进行。采用Mastersizer 2000型激光粒度分析仪测定土壤粒径分布,即称取过2 mm筛的土样约0.35 g于烧杯中,加入10 ml的10%双氧水溶液去除有机质,用电热板加速充分反应,加入10 ml的10%盐酸溶液去除碳酸钙。注满蒸馏水并静置12 h后抽出上清液,加入10 ml的0.06 mol/L六偏磷酸钠溶液分散土粒,超声振荡15 min,用粒度仪测得土壤粒径体积分数。
1.2.2 土壤PSD单重分形维数计算
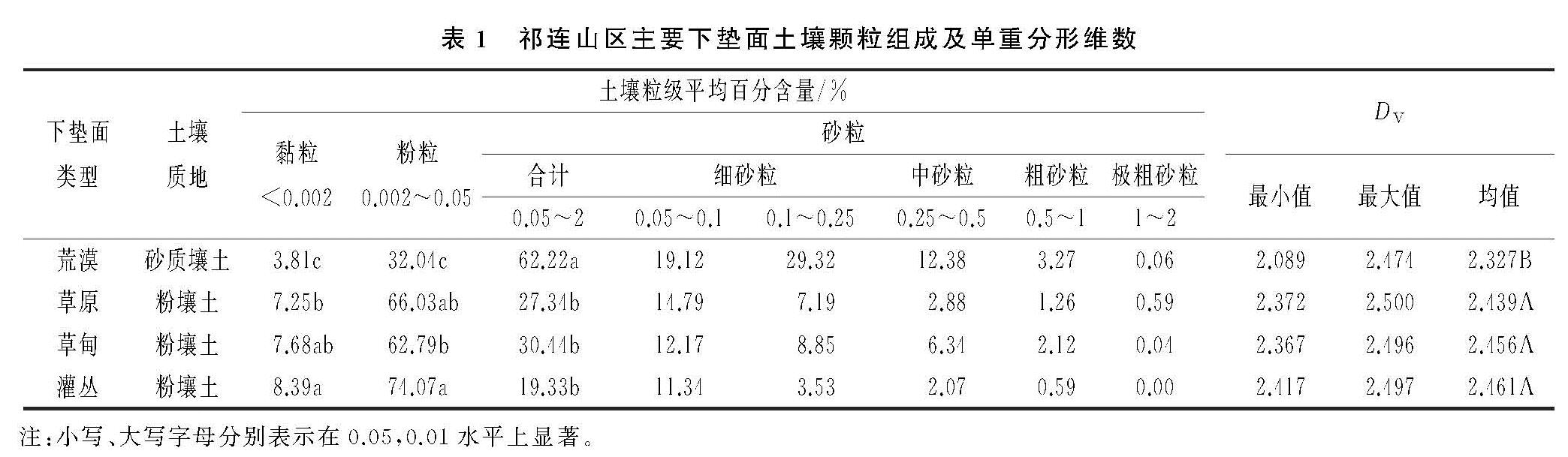
土壤粒径体积分数由美国土壤质地分级标准被划分为7个等级见表1,土壤PSD的单重分形维数(DV)[8]计算如下:
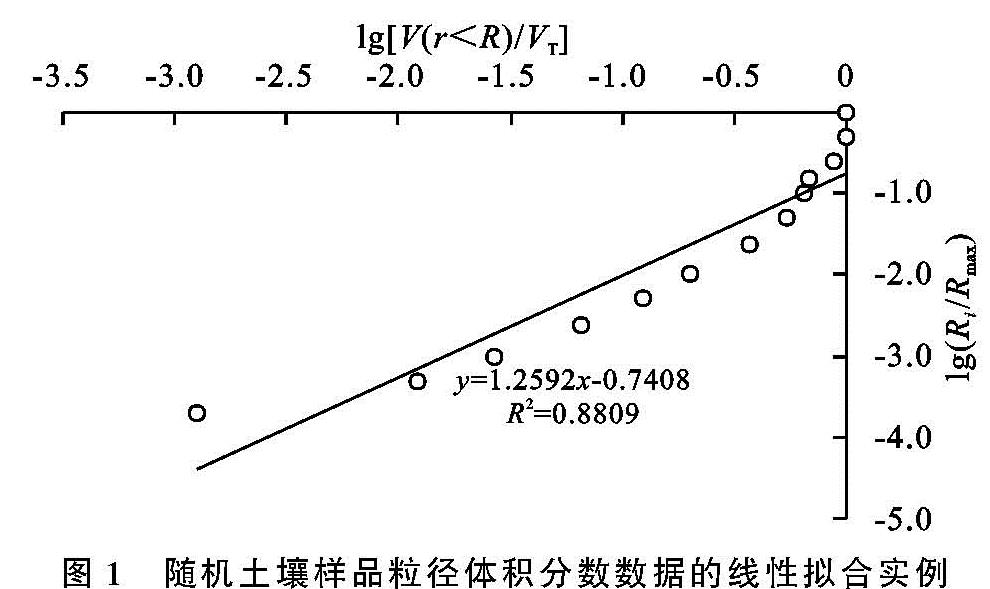
(V(rT)=((R)/(Rmax))3-DV(1)
式中:R为土壤某特定粒径; V(rT为土粒总体积分数; Rmax为最大粒径,公式(1)两边同时取对数,并对试验数据进行线性回归拟合,通过拟合曲线获得斜率K值,则3-K得到DV(图1)。
1.2.3 土壤PSD多重分形维数计算
由激光粒度仪测得的连续分布的土壤PSD数据,采用对数等差递增法,将粒径测度区间I=[0.5,1 000]划分成64个小区域I1=[Φi,Φi+1],其中lg(Φi+1/Φi)=0.052。通过对数转换构建一个无量纲区间J=[0,lg(1000/0.5)]=[0,3.301],采用二进制划分法,区间J分别被N(ε)=2k(k=1,2,3,4,5,6)划分为同尺度ε的子区间Ji,即分别被2,4,8,16,32,64等分,尺度ε=3.301*2-k(ε=1.650,0.825,0.413,0.206,0.103,0.052)。土壤多重分形维数D(q)的计算[17]如下:
D(q)=limε→01/(q-1)·(lg[∑N(ε)i=1μi(ε)q])/(lgε)(q≠1)(2)
D1=limε→0(∑N(ε)i=1μi(ε)lgμi(ε))/(lgε)(q=1)(3)
式中:D1为信息维数; μi(ε)为各等分子区间Ji内所有Vi之和; Vi=vi/Σvi; vi为各区间内土粒体积分数; q为实数。
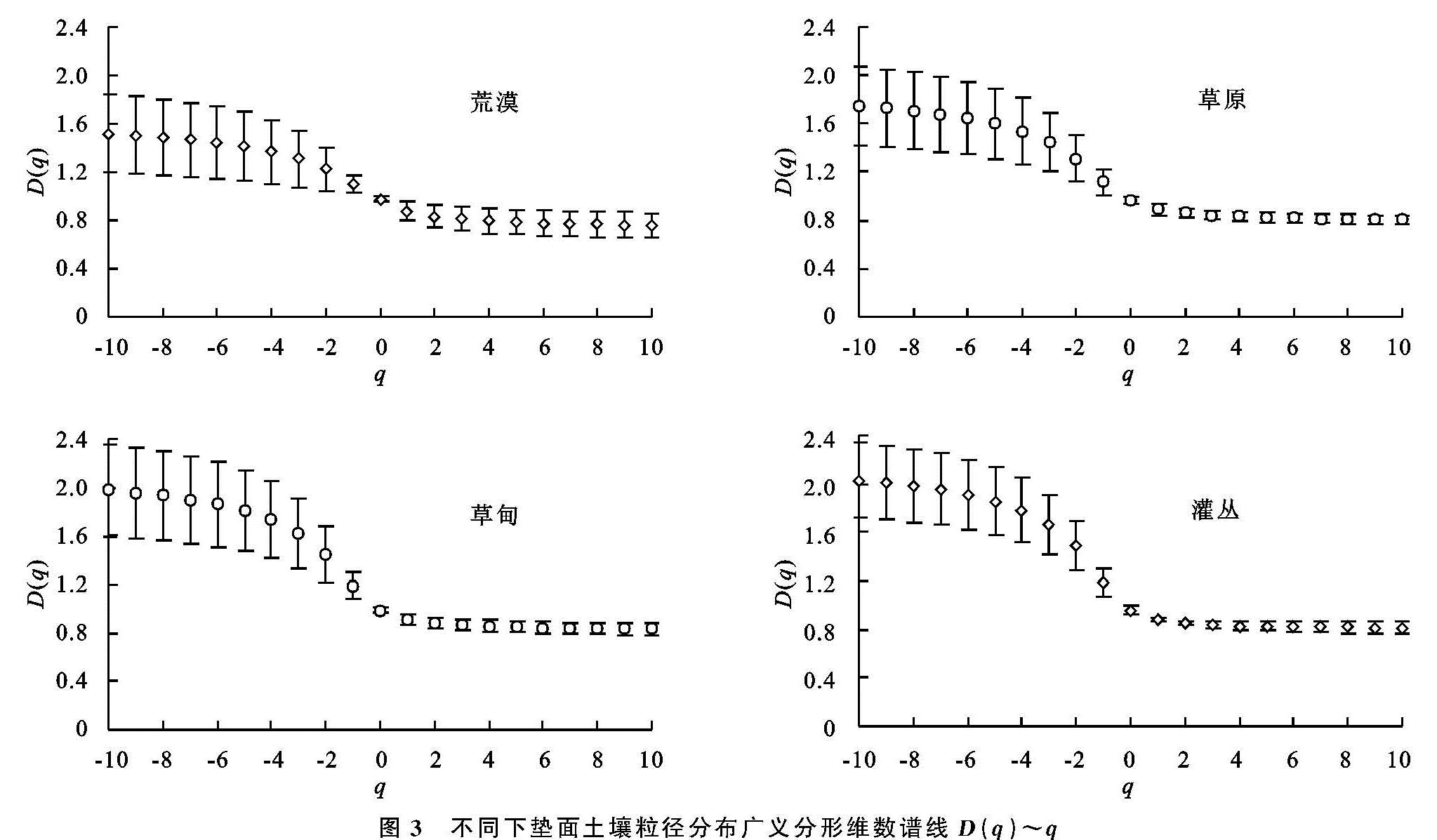
由多重分形维数理论可知,D(q)是不同层次上分形测度的统计参量,绘制的广义维谱曲线D(q)~q用于量化土壤颗粒分形结构的复杂度和非均匀性[6]。即q<0时D(q)变化幅度(D-10-D0)越大,反映了土壤PSD范围越宽,土壤分形结构越复杂; q>0时D(q)变化幅度(D0-D10)越大,反映了土壤PSD越不均匀。由公式(2)和(3)计算可得,当q取0,1,2时,D(q)分别是D0,D1和D2等多重分形参数,即D0是容量维数,提供土壤PSD的最基本信息,值越大表明土壤PSD范围越大或缺失粒径越少[4,17]。信息维数D1和D1/D0主要反映土壤PSD测度的集中度,值越大表明土壤PSD的集中度越低,D1/D0还能反映土壤PSD的异质度,其值越接近0或1,分别表明土壤PSD主要集中在稀疏区或密集区[6]。D2是关联维数,反映土壤粒径在局域区间测度的均匀性,值越大表明土壤PSD越均匀。