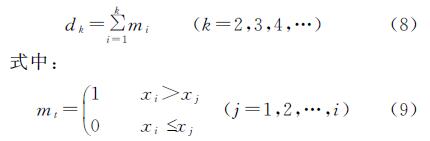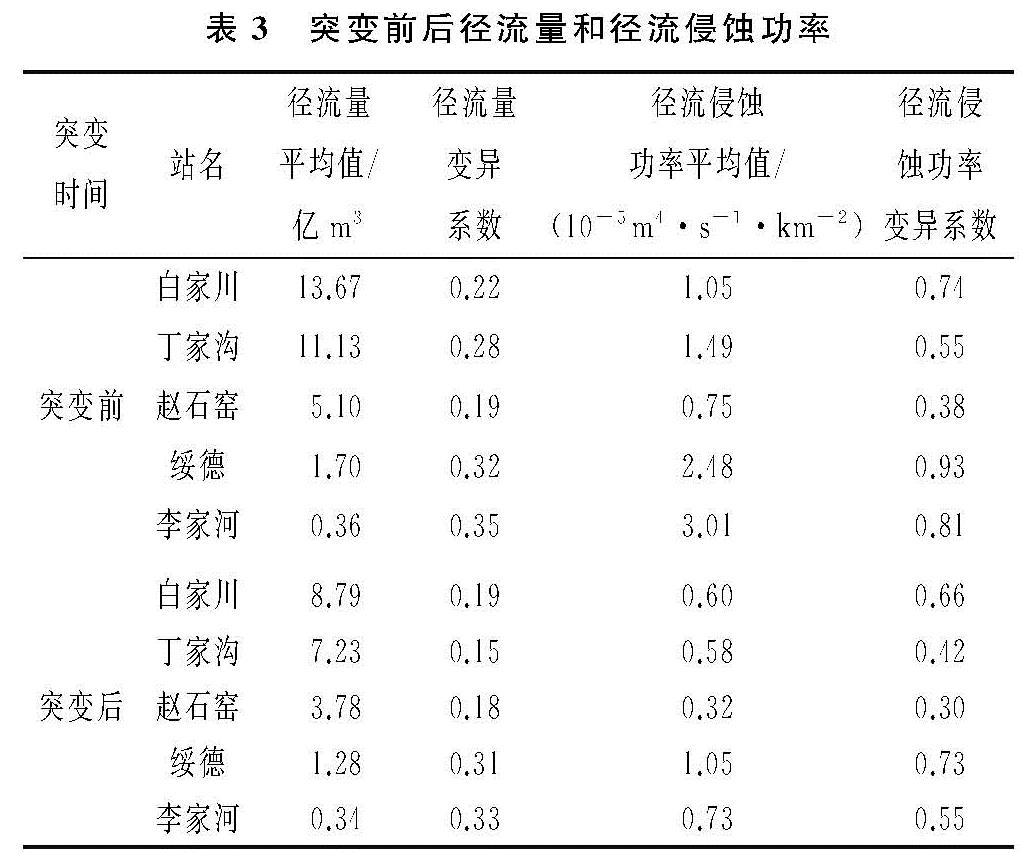
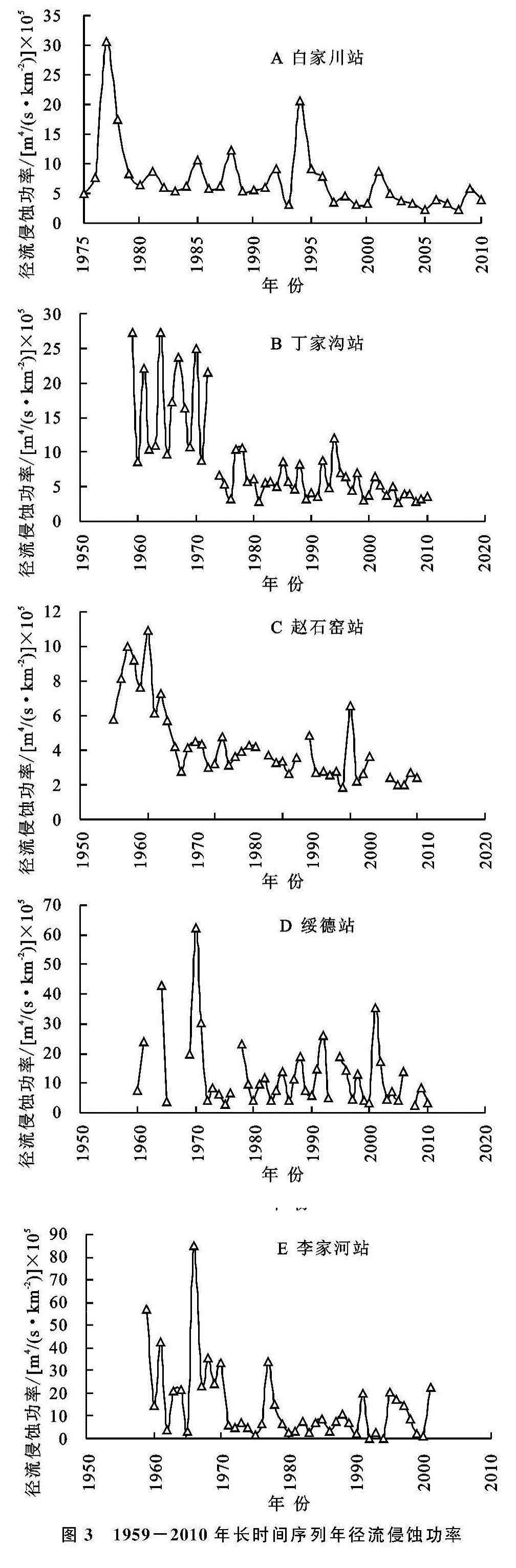
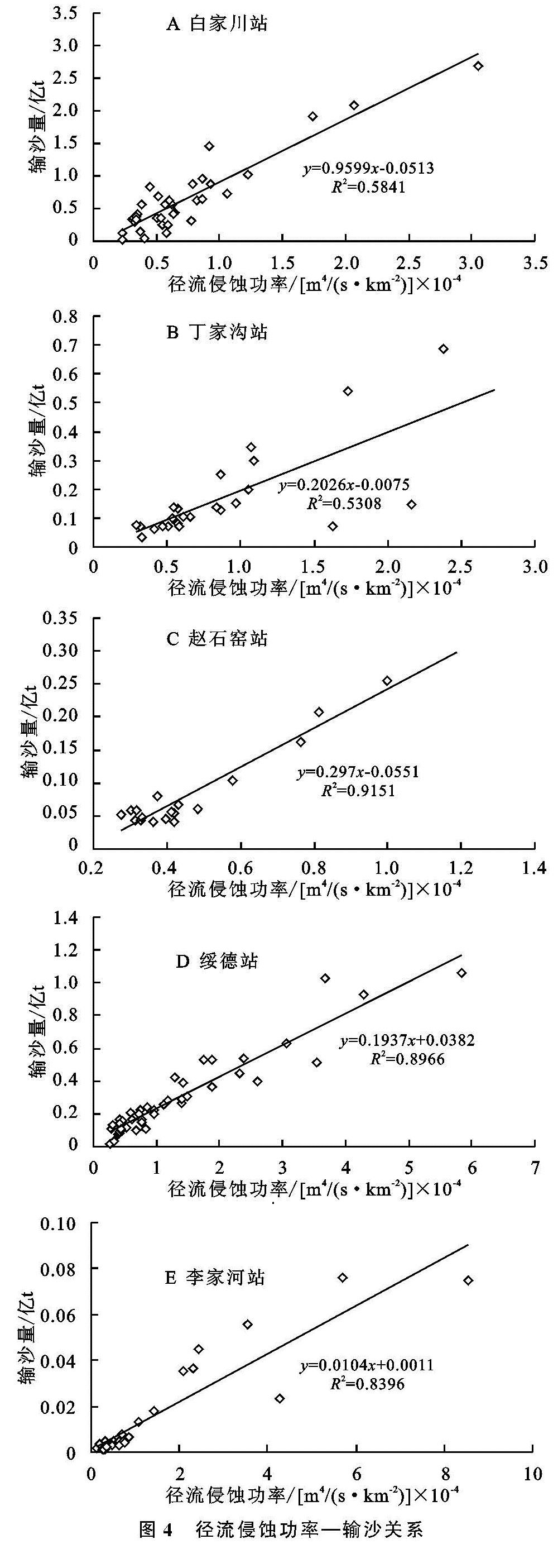
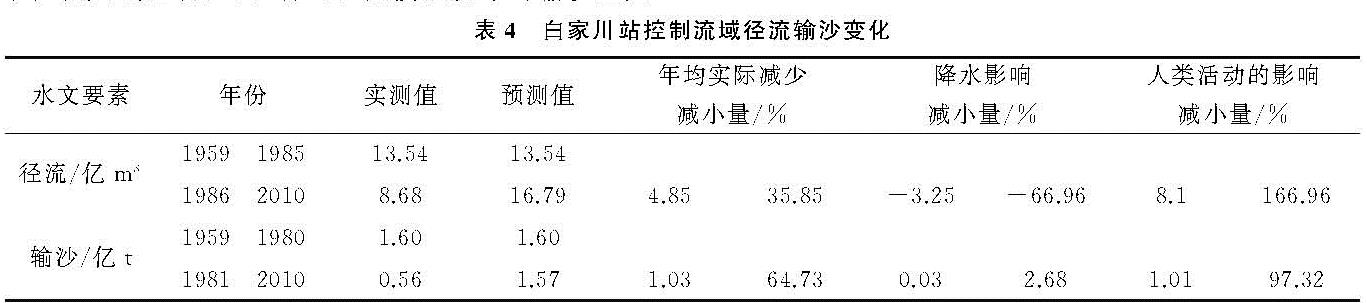
本文所用的水文资料来源于黄河水文年鉴中1956—2010年的水文资料,选取无定河流域5个代表水文测站李家河站、绥德站、赵石窑站、丁家沟站和白家川站(图1),各代表站分别控制小理河流域、大理河流域、无定河赵石窑站以上流域、无定河丁家沟站以上流域、无定河流域,控制流域面积分别为807 km²,3 893 km²,15 325 km²,23 422 km²,29 662 km²。

图1 无定河流域位置及水文站点分布

目前,在研究径流侵蚀方面主要有剪切力模型和侵蚀能量模型两大类^[11-14],本文采用侵蚀能量模型中的径流侵蚀功率理论。

通过以下公式计算出径流侵蚀产沙的侵蚀动力指标:

E=Q'_mH=W/A(Q_m)/A=W/(A²)A'(Q_m)/(A')

=(A')/(A²)WV=(A')/(ρgA²)ρgWV=(A')/(ρgA²)FV(1)

令Con=(A')/(ρgA²),则:

E=Con·F·V(2)

式中:W为径流总量(m³); A为流域面积(m²); Q_m为洪峰流量(m³/s); A'为与Q_m对应的流域出口断面的过水面积(m²); V为流域出口断面与Q_m对应的平均流速(m/s); ρ为水的密度(kg/m³); g为重力加速度(m/s²); F为作用力(N)。

可以看出,指标E具有功率的量纲。本文将径流年内分配试作一次径流过程^[15],通过使用径流侵蚀功率的计算公式,计算出年径流侵蚀功率,从年尺度上研究流域径流侵蚀功率的时空变化特征。

则以下式中:各项含义分别为:

E_a=Q'_m·H(3)

式中:E_a为年径流侵蚀功率[m⁴/(s·km²)]; H为月平均径流深(m); Q'_m为最大月平均流量模数[m³/(s·km²)],其大小等于最大月平均流量与流域面积的比值。

本文采用Mann-Kendall非参数秩次相关检验法^[16]来进行水沙变化趋势分析。可构造统计量:

式中:

τ=(4∑ⁿ_i=1p_i)/(n(n-1))(5)

var(τ)=(2(2n+5))/(9n(n-1))(6)

统计量U称为Kendall秩次相关系数,当n增加时,U将很快收敛于标准正态分布。给定显著性水平α,其双尾检验临界值为U_α/2,当|U|α/₂时,系列趋势不显著,资料一致性较好; 当|U|>U_α/2时,系列趋势显著,如U>0,系列呈上升趋势,如U<0,系列呈下降趋势。

线性回归法通过建立年径流序列y_t与相应的时序t之间的线性回归方程来检验时间序列的线性变化趋势^[17-18]。线性回归方程为:

y_t=at+b(7)

式中:y_t为实测序列; t为时序(t=1,2,…,n; n为序列长度); a为斜率,表征时间序列的平均趋势变化率; b为截距。

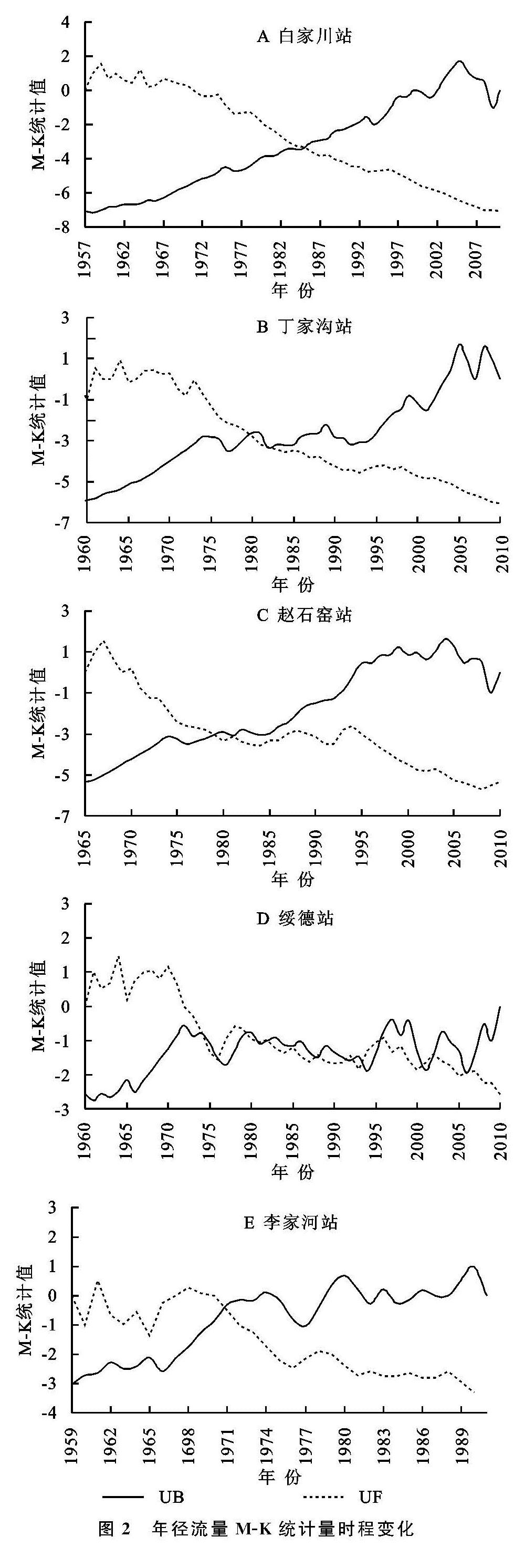
Mann-Kendall突变点诊断法被用于进行突变年份的检验。当Mann-Kendall法用于检验序列突变性时^[19],需构造一个秩序列d:

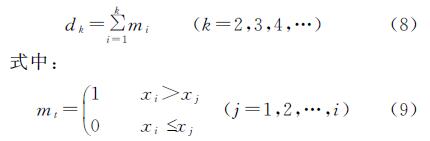
在时间序列随机独立的假定下,d_k的均值和方差可由下边两个式子计算:

E(d_k)=(k(k-1))/4(10)

var(d_k)=(k(k-1)(2k+5))/(72)(11)

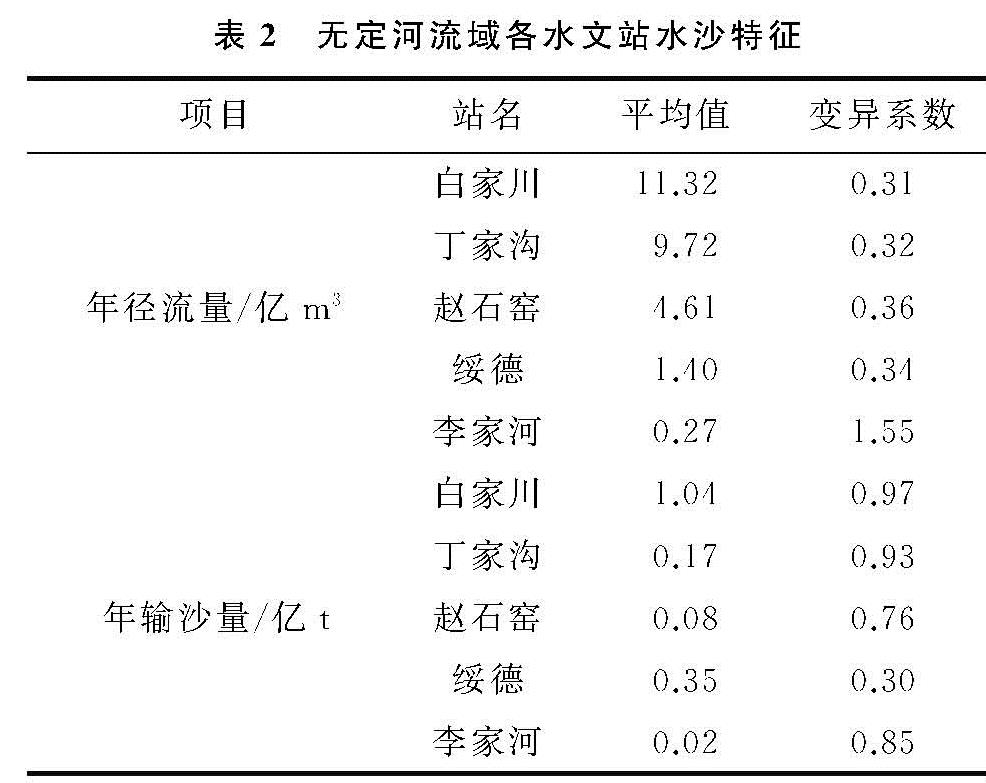
定义统计变量

按时间序列逆序,再重复上述过程,同时使UB_L=-UF_K(L=n+1-k),由UF_K绘制出曲线C₁,由UB_L绘制出曲线C₂。若UF_K或UB_L的值超过临界直线,表明序列上升或者下降趋势显著。如果C₁或C₂出现交点,且交点在临界线之内,那么交点对应的时刻便是突变开始的时间。

通过运用M-K非参数秩次相关检验,计算5个代表水文站径流变化趋势特征,见表1。可以看出,无定河流域空间内各小流域径流量均发生了显著变化。径流量秩检验系数都为负数,径流量呈下降趋势,且绝对值随流域面积逐渐增大:白家川>丁家沟>赵石窑>绥德>李家河,无定河干流水文站显著水平0.001,支流水文站显著水平0.05,干流下降趋势比支流更显著。

表1 年径流量变化趋势M-K非参数秩次相关检验

使用M-K检验法对无定河流域白家川站、丁家沟站、赵石窑站、绥德站、李家河站等5个水文站的年径流系列进行突变点检验,检验结果见图2。5个水文站的径流变化呈减小趋势,趋势明显超过α=0.05。由图中选取第一个交点作为突变点进行分析,可以看出,白家川站年径流系列突变点在1985年左右,丁家沟站年径流系列突变点在1979年左右,赵石窑站年径流系列突变点在1978年左右、绥德站年径流系列突变点在1974年左右,李家河站年径流系列突变点在1971年左右; 说明大理河流域最早受人类活动影响,大理河一级支流小理河流域受人类活动影响更早。

图2 年径流量M-K统计量时程变化

表2 无定河流域各水文站水沙特征

表3 突变前后径流量和径流侵蚀功率

由表3可以分析出,突变年份后无定河流域白家川站、丁家沟站、赵石窑站、绥德站、李家河站等5个水文站径流量的平均值、变异系数等统计特征值基本小于突变年份之前,说明突变年份后的径流系列更为稳定,同时与表2对比,发现突变年份之前的水文要素统计特征指标值比总体统计特征指标值大,突变年份之后的水文要素统计特征指标值比总体统计特征指标值小。

图3 1959-2010年长时间序列年径流侵蚀功率

图4 径流侵蚀功率—输沙关系

通过使用径流侵蚀功率理论,计算出了无定河流域5个水文站1956—2010年的年径流侵蚀功率,见图3。由图3可以看出,5个站点的径流侵蚀功率时间序列都呈下降减小趋势; 通过统计发现白家川站、丁家沟站、赵石窑站、绥德站、李家河站的5个水文站控制流域的径流侵蚀功率的标准差等统计值,在各自径流量突变年份之前都大于突变年份后,突变年份之前流域年径流侵蚀功率平均标准差高于突变年份后,这说明突变后的侵蚀功率更为稳定。

通过对白家川站、丁家沟站、赵石窑站、绥德站和李家河站5个水文站1959—2010年长时间序列径流侵蚀功率取平均值,以及在各自突变年份之前取平均值和突变年份之后取平均值,可以分析出,无定河流域白家川站、丁家沟站、赵石窑站、绥德站和李家河站的平均径流侵蚀功率分别为0.73,1.03,0.68,2.50,18.73。随着控制流域尺度的增加呈递减小趋势,无定河支流大理河流域绥德站和小理河流域李家河站的平均径流侵蚀功率大于干流; 流域平均径流侵蚀功率随着控制流域尺度的增加呈递减小趋势。突变年份之后年平均径流侵蚀功率比突变年份前平均减少1.05*10^-4 m⁴/(s·km²),且支流径流侵蚀功率大于干流,干流侵蚀功率变化基本趋于稳定,突变年份前无定河流域白家川站、丁家沟站、赵石窑站、绥德站和李家河站的年平均径流侵蚀功率随着流域尺度增大而逐渐减小的变化规律比较明显,突变年份后无定河流域白家川站、丁家沟站、赵石窑站、绥德站和李家河站的年平均径流侵蚀功率均有所减少,随着流域尺度增大变化规律比较不明显。

通过对无定河流域5个代表水文站的年输沙量与年径流侵蚀功率线性拟合,结果见图4。根据曲线分析,无定河流域白家川站、丁家沟站、赵石窑站、绥德站、李家河站径流侵蚀功率与输沙量相关关系如图4,可以看出,径流侵蚀功率与输沙量呈线性关系,输沙量随着径流侵蚀功率的增大而增大,5个代表水文站大部分径流侵蚀功率与输沙量的关系点均密集分布在相关线左右,可以看出径流侵蚀功率与输沙量关系没有出现系统性的偏离,线性相关方程R²分别为0.85,0.53,0.92,0.90,0.89,说明了径流侵蚀功率理论在流域年尺度上能更好的表征径流侵蚀输沙关系。